Multiplication as repeated addition
March 24, 2020
Repeated addition as a model for multiplication persists in being the dominant introductory model for multiplication in many curricula. Since I have recently been reading a lot from Vasily Davydov, I have come across his critique of multiplication as repeated addition. The details of this have been discussed by others*. I will instead suggest some situations, which school children are familiar with, in which the addition model is not apparent.
Combinatorial mathematics
A child has 3 different colour hats, 4 different colour scarves and 3 different colour wellies. How many combinations of hats, scarves and wellies are possible?
The solution here is found by: 3 × 4 × 3
Scaling pictures on the computer

Children in upper primary are largely familiar with scaling problems, the picture can become x times bigger, but there is no obvious addition structure here.
Fractional multiplication
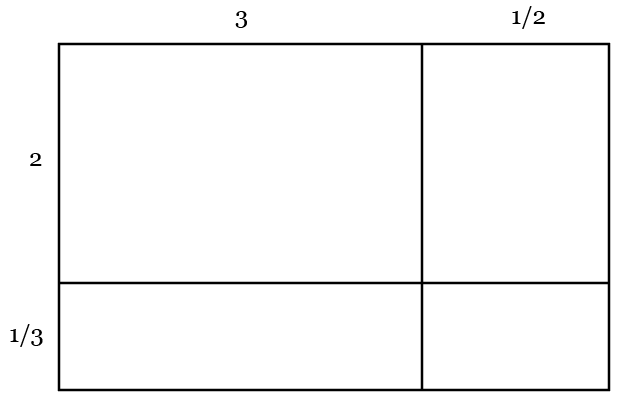
Here, the additive structure works for adding different parts of the grid. But notice that evaluating 1/2 × 1/3 draws upon a scaling or non-additive understanding of multiplication.
Converting money or time
Converting an amount of euros into sterling will present a non additive structure of multiplication.
Change of units for a large difficult to count amount
Davydov's example for multiplication without an additive structure was to suggest the problem of trying to find out how many sweets in a bag. If counting a big bag, the counting would be cumbersome. The situation calls for a change in units, whereby the bag of sweets is weighed and so is one sweet, therefore yielding a multiplication relationship between the amounts
*Literature which discusses why multiplication is not well represented by repeated addition:
- Children doing mathematics, Nunes and Bryant
- Psychological abilities of primary school children in learning mathematics, Davydov
- Where mathematics comes from, Lackoff and Nunes
Balance, inequality, equality – L’altalena by Enzo Mari
March 17, 2020
Cuisenaire… what next!?
November 28, 2019
This year I am working with multiple teachers on the Gattegno method in classrooms. The conversation we often have is around what to do next after each exploration with the rods in the classroom.
We have read and understood passages from Goutard's Mathematics and Children. And, also referred to the article from Caroline Ainsworth on her research on work with Cuisenaire. To try to distil this into some sort of progression, we took the phases of working with the rods suggested by Goutard, and also referenced by Ainsworth, and then noted what we thought they looked like in terms of what children needed to understand and know.
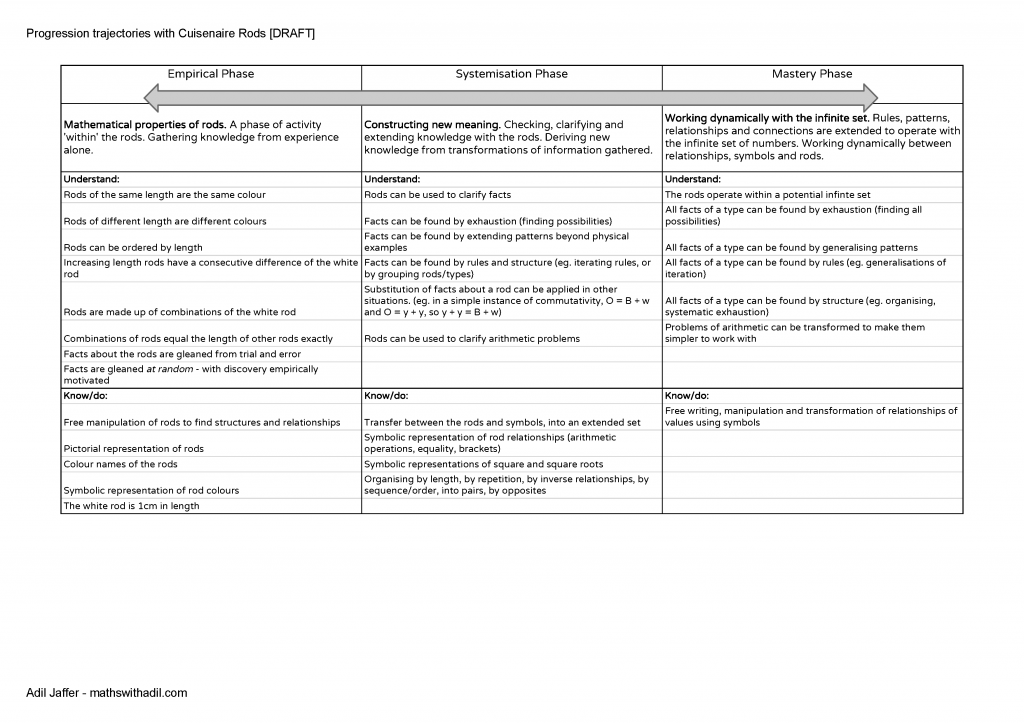
This is our current draft. It's a live document at this moment and perhaps should remain a live/draft in the longer term. It has worked for us when making choices and listening to proposals from children about what next we can do as a class.
So for example, one class has had plenty of play with the rods and has discovered a lot of understanding from the empirical phase. However, my colleague and I wanted draw attention to fact that all rods were equivalent to combinations of other rods. Hence, our proposal last week was to make walls with the following rules for lines in the wall:
- Each line needs to be horizontal
- Lines should be unique (no repeats)
- All gaps should be filled to the exact size of the walls
This generated walls with every combination of rods for the size of the longest rod. After some lessons on this, we moved forward to explore how a rule might change the walls and activity. We added an extra rule: there should be exactly 2 rods in each line.
My colleague and I noticed that the lines were being organised in pairs of opposite combinations. For example, in the yellow wall, we would see red green and then green red on the next line.
This morning we started our lesson by talking about organising. Children felt it was good to be organised(!) and we noted some examples from home and the classroom:
- organising the pencils by colour
- organising our clothes to be ready
- organising the rods by colour
- organising the rods by length
One thing my colleague and I were keen on were to see if we could work with the children to notice that walls could be organised by length. We used the same rule as in the previous lesson, having exactly 2 rods in each line. After some exploration and then spotting how we were organising our lines we decided we needed to suggest that children build walls which organised the rods by length. As a pedagogic choice, we felt it was right to offer the proposal since it was not going to come from the children at that moment.

Feeling that this is the right thing to do is often difficult. Especially when working as a teacher and knowing that the philosophical persuasion of the schools is that of being led by children's proposals. I'm still unsure that it was the right decision! Should we have been patient and waited for the children? One thing I share with staff at my school is an excerpt from Alan Wigley's 1992 ATM article on teaching models.
Reading this gets me back to a point of trying to enjoy the tension of pedagogic choices in a moment.
With the above document to help us stay on track, we feel good too, knowing that the progression is there.
Flipping rod trays
November 9, 2018
Proposal: make patterns using the trays
Reflection students:
We were going to make some patterns. We made the two patterns in the trays. We were testing how to flip over the Minecraft (rods). We flipped over the pattern, it went into the other plate and it stayed there. We thought that the pattern would break but it didn’t.
This side is over here, but not over here (talking about the orange and blue rods on the side). When we flipped it, it went on the other side, we had no idea that would happen.
My first pattern had a line it went: green, red, green, red, green, red and the flipped one it came red, green, red, green, red, green. And on another line it was orange, white, blue and then it became blue, white, orange.
V and V
I will share this exploration with the class next week and we will explore what is happening when we flip tray patterns.
Embodied mathematics & movement work with children
November 6, 2018
So in 2014, I came across Where Mathematics Comes From by Lakoff and Nunez. The book contains some simple statements which caught my attention:
- let’s go back to square 1
- let’s go forwards a couple steps
- there’s zero in the refrigerator
- this nullifies all that we have done
- Fred and Ginger danced as one
These metaphors imply that we understand numbers to operate as objects do or as movement does. These metaphors fascinated me and led me down a path to wanting to work with younger learners to understand how ideas of number are first experienced by learners. Several years on, I'm working with 6 year olds - a big change from 11-16 year olds back in the UK - and I've began working on trying to realise what these embodied metaphors mean for the learning of the mathematics which Lakoff and Nunez map these embodied metaphors to.
Last academic year, I worked with two movement (dance) teachers in my school and my class of 22 children. We spent an hour a week over 8 weeks with my class with the intention of supporting children to gain a deeper understanding of number using movement as a starting point.
Our basic lesson included a warm-up, proposals to the children to make a locomotor motion along with a drum pattern and then an invitation to draw the movements they had made on a roll of paper. We did this for about 6 weeks of the 8, allowing time for the class a couple lessons to learn the workings of the dance studio. Here are some drawings from 2 lessons.
Lesson 3 from 8:
Proposal: move to the drum (teacher counted and hit the drum from 1 to 8)
After the movement session we thought about the number pathways which we made with our bodies. The class were keen to make up some new pathways they could try out. And also tried to move to each other's drawn pathways.
One suggestion from a class member was to move more than one step at a time and so they drew pathways which showed jumps through space, using different numbers.
We had some discussion around numbers and what they were and different ways in which we experience them.
One student remarked:
When I was in group 2, I thought numbers were symbols that meant how many there were.
We had also previously established that numbers were symbols, words, names of numicon shapes and also meant how many once a set of objects was counted.
On another day, I asked the class: 'What is five?'
These responses included metaphors of movement.
It could be a pathway of 5. That it could go zig-zag then straight then curve then straight again.
Like this, this, this and then that (showing with her hands a movement).
5 is a pathway and a story.
Lesson 5 from 8:
Proposal: From a starting position, move 2 beats forwards. Move 6 beats backwards.
The first image in the selection of drawings was something we spoke about afterwards as a class. We then all tried to move the same pattern as the student who drew it. We talked about negative numbers and then made some more movements back in our classroom which explored forwards from the origin point (starting position) and then backwards through the origin.
From January, I intend to undertake the project again with my new class. Until then I have some reading and planning to carry out, to think about how the project extends into the classroom further. And to shape up more ideas of the role of movement in mathematics learning.
I really want to figure out which tasks can be set for students which can be carried out as group work. And which of these tasks lead to explorations and new realisations about the structure of the number system. I'm particularly excited by explorations of negative numbers and non-whole numbers; the latter was explored last year, but I don't have good documentation from those explorations which I can share.
Writing
November 2, 2018
I've had some excellent conversations recently with a colleague about how we achieve the holy grail of free writing from work with Cuisenaire Rods recently. We have looked at the work done by Gattegno and Goutard and Caroline Ainsworth and are trying to figure out how we make that work for our setting.
My colleague this week introduced notebooks for her class for their discoveries with rods. The invitation is for them to keep a note of their discoveries with the rods. Not missing a trick, I decided to do the same with my class.
We first spoke about discoveries from scientists and what they do with them. We talked about our discoveries with the rods and how we should remember them. Once motivated to keep a record of their discoveries, we got to trying to note them down in new special books for discoveries.
Children were encouraged to use whatever worked for them: pictures, words or symbols. We worked on writing without access to the concrete materials; this was a suggestion from Goutard. To work on the internalised and remembered structures and not to merely describe the concrete in front of them.
Here are 3 examples:
Six land
November 1, 2018
I'm a huge fan of Six-land, as proposed by Andrew Jeffrey. It is an imagined land in which things work in base-6. I worked with a group of children from a mix of classes (aged 6-8) and we have been figuring out how the number system works in six-land and also how to measure things.
One of the conversations we had was about how children who lived in six-land, learn how to use their numbers. A child suggested they had counting books... so we made some! Books that count in base-6. One of my favourites was one from a group who counted rocks and other natural things and made their book by photocopying them.

Equivalence game
November 1, 2018
Stolen from twitter: a game of equivalences using symmetry. Each student places a train of rods and then their partner aimed to place an equivalent train on their own side. I was surprised at how challenging this was for some students.
Representing my famalam
October 10, 2018
Taking another task from the ATM Cuisenaire material, I asked the children in the class to pick 3 rods; each representing papa bear, mama bear and baby bear from Goldilocks and Three Bears. They were to hide the rods behind their backs and reveal the correct rod for each character as they came up in the story when being read aloud. This was fun. So we then thought about how to represent our own families with the rods. As well as other people outside our family.
Some good estimation and more accurate representations of the rods is happening here. I hope this leads to the children noticing that we can record our play with the rods and keep it for future.
We then listened to this song... (maybe)
Representin’ ain’t easy
October 4, 2018
I thought I'd try out a task from the Cuisenaire booklet from ATM. It's called sandwiches and the rough proposal to children is to make sandwiches (from the rods) and then ask a friend to find the missing rod from a full sandwich. This proposal was liberally followed by children in my class today. And so was the part of noting the sandwiches made onto paper. Many definitely didn't see the 1 to 1 correspondence in size of squares on paper to the size of the rods. I found this quite surprising. Nevertheless, I think it is a worthwhile step en route to free writing with the rods.