Multiplication as repeated addition
Repeated addition as a model for multiplication persists in being the dominant introductory model for multiplication in many curricula. Since I have recently been reading a lot from Vasily Davydov, I have come across his critique of multiplication as repeated addition. The details of this have been discussed by others*. I will instead suggest some situations, which school children are familiar with, in which the addition model is not apparent.
Combinatorial mathematics
A child has 3 different colour hats, 4 different colour scarves and 3 different colour wellies. How many combinations of hats, scarves and wellies are possible?
The solution here is found by: 3 × 4 × 3
Scaling pictures on the computer

Children in upper primary are largely familiar with scaling problems, the picture can become x times bigger, but there is no obvious addition structure here.
Fractional multiplication
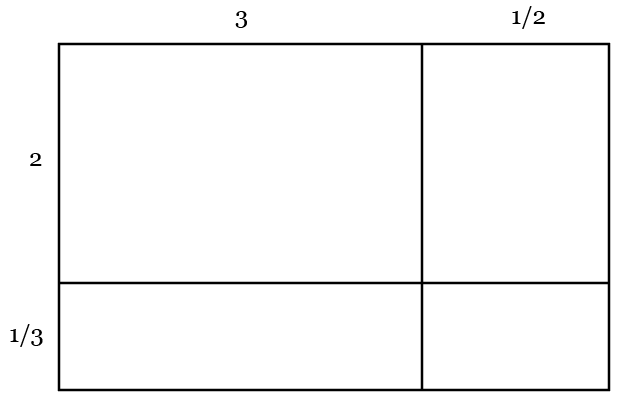
Here, the additive structure works for adding different parts of the grid. But notice that evaluating 1/2 × 1/3 draws upon a scaling or non-additive understanding of multiplication.
Converting money or time
Converting an amount of euros into sterling will present a non additive structure of multiplication.
Change of units for a large difficult to count amount
Davydov's example for multiplication without an additive structure was to suggest the problem of trying to find out how many sweets in a bag. If counting a big bag, the counting would be cumbersome. The situation calls for a change in units, whereby the bag of sweets is weighed and so is one sweet, therefore yielding a multiplication relationship between the amounts
*Literature which discusses why multiplication is not well represented by repeated addition:
- Children doing mathematics, Nunes and Bryant
- Psychological abilities of primary school children in learning mathematics, Davydov
- Where mathematics comes from, Lackoff and Nunes

