Cuisenaire... what next!?
This year I am working with multiple teachers on the Gattegno method in classrooms. The conversation we often have is around what to do next after each exploration with the rods in the classroom.
We have read and understood passages from Goutard's Mathematics and Children. And, also referred to the article from Caroline Ainsworth on her research on work with Cuisenaire. To try to distil this into some sort of progression, we took the phases of working with the rods suggested by Goutard, and also referenced by Ainsworth, and then noted what we thought they looked like in terms of what children needed to understand and know.
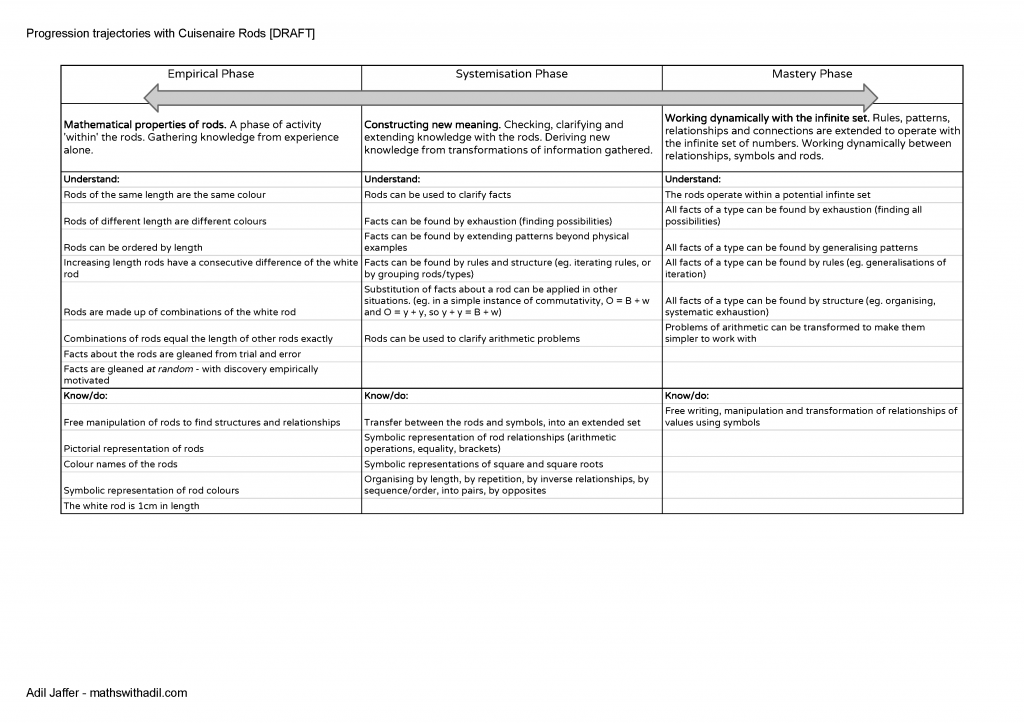
This is our current draft. It's a live document at this moment and perhaps should remain a live/draft in the longer term. It has worked for us when making choices and listening to proposals from children about what next we can do as a class.
So for example, one class has had plenty of play with the rods and has discovered a lot of understanding from the empirical phase. However, my colleague and I wanted draw attention to fact that all rods were equivalent to combinations of other rods. Hence, our proposal last week was to make walls with the following rules for lines in the wall:
- Each line needs to be horizontal
- Lines should be unique (no repeats)
- All gaps should be filled to the exact size of the walls
This generated walls with every combination of rods for the size of the longest rod. After some lessons on this, we moved forward to explore how a rule might change the walls and activity. We added an extra rule: there should be exactly 2 rods in each line.
My colleague and I noticed that the lines were being organised in pairs of opposite combinations. For example, in the yellow wall, we would see red green and then green red on the next line.
This morning we started our lesson by talking about organising. Children felt it was good to be organised(!) and we noted some examples from home and the classroom:
- organising the pencils by colour
- organising our clothes to be ready
- organising the rods by colour
- organising the rods by length
One thing my colleague and I were keen on were to see if we could work with the children to notice that walls could be organised by length. We used the same rule as in the previous lesson, having exactly 2 rods in each line. After some exploration and then spotting how we were organising our lines we decided we needed to suggest that children build walls which organised the rods by length. As a pedagogic choice, we felt it was right to offer the proposal since it was not going to come from the children at that moment.

Feeling that this is the right thing to do is often difficult. Especially when working as a teacher and knowing that the philosophical persuasion of the schools is that of being led by children's proposals. I'm still unsure that it was the right decision! Should we have been patient and waited for the children? One thing I share with staff at my school is an excerpt from Alan Wigley's 1992 ATM article on teaching models.
Reading this gets me back to a point of trying to enjoy the tension of pedagogic choices in a moment.
With the above document to help us stay on track, we feel good too, knowing that the progression is there.

