Multiplication as repeated addition
Repeated addition as a model for multiplication persists in being the dominant introductory model for multiplication in many curricula. Since I have recently been reading a lot from Vasily Davydov, I have come across his critique of multiplication as repeated addition. The details of this have been discussed by others*. I will instead suggest some situations, which school children are familiar with, in which the addition model is not apparent.
Combinatorial mathematics
A child has 3 different colour hats, 4 different colour scarves and 3 different colour wellies. How many combinations of hats, scarves and wellies are possible?
The solution here is found by: 3 × 4 × 3
Scaling pictures on the computer

Children in upper primary are largely familiar with scaling problems, the picture can become x times bigger, but there is no obvious addition structure here.
Fractional multiplication
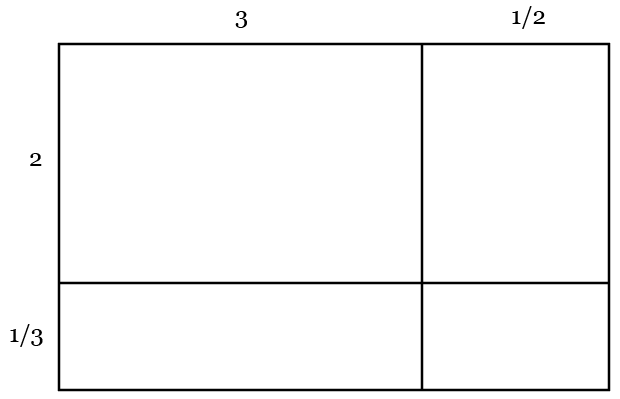
Here, the additive structure works for adding different parts of the grid. But notice that evaluating 1/2 × 1/3 draws upon a scaling or non-additive understanding of multiplication.
Converting money or time
Converting an amount of euros into sterling will present a non additive structure of multiplication.
Change of units for a large difficult to count amount
Davydov's example for multiplication without an additive structure was to suggest the problem of trying to find out how many sweets in a bag. If counting a big bag, the counting would be cumbersome. The situation calls for a change in units, whereby the bag of sweets is weighed and so is one sweet, therefore yielding a multiplication relationship between the amounts
*Literature which discusses why multiplication is not well represented by repeated addition:
- Children doing mathematics, Nunes and Bryant
- Psychological abilities of primary school children in learning mathematics, Davydov
- Where mathematics comes from, Lackoff and Nunes
Balance, inequality, equality - L'altalena by Enzo Mari
There are lots of blogs and websites which highlight children's books with mathematical ideas in them. And we have lots of those books in my school. I also like to find books which are not especially made for children but can be great for teaching.
L'altalena by Enzo Mari is one such book and is about balancing animals. We were able to source a few copies in the Netherlands from a local book shop. And ideabooks is a good starting point if you are hoping to find a copy outside the NL.
Enzo Mari is a renowned product designer and had initially made the animals as an oak puzzle. We were able to source a set.
The animals are fun to sort out, to order by size, to talk about straight and curved body parts, to talk about heavier and lighter, to talk about equality and inequality. The children like to make stories about the animals coming onto the see-saw (we have a plank of wood)... and they like to see them fall down. Which is a bit terrifying since the shapes are so beautifully made! Soon I might get them cut out as stamps so that the children can make their own see-saw books, I have been able to make some cut files for laser cutting these out of foam... so that will be fun!
Since many playgrounds no longer have see-saws, having one in the classroom seems to be a must. Scales can help here, but taking a plank of wood and balancing it is a massive idea for our children to get hands on with. And these wooden shapes have a lot of story making potential for children.
These are listed on other websites, but we have found these books to have really obvious links to the one by Enzo Mari too:
- Balancing Act, Ellen Walsh
- How Much Does a Ladybug Weigh, Alison Limentani
- Just a Little Bit, Ann Tompert
Get in touch if need some help on getting the animal puzzle.










