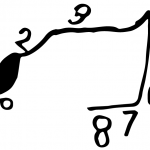
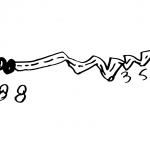
Flipping rod trays
Proposal: make patterns using the trays
Reflection students:
We were going to make some patterns. We made the two patterns in the trays. We were testing how to flip over the Minecraft (rods). We flipped over the pattern, it went into the other plate and it stayed there. We thought that the pattern would break but it didn’t.
This side is over here, but not over here (talking about the orange and blue rods on the side). When we flipped it, it went on the other side, we had no idea that would happen.
My first pattern had a line it went: green, red, green, red, green, red and the flipped one it came red, green, red, green, red, green. And on another line it was orange, white, blue and then it became blue, white, orange.
V and V
I will share this exploration with the class next week and we will explore what is happening when we flip tray patterns.
Embodied mathematics & movement work with children
So in 2014, I came across Where Mathematics Comes From by Lakoff and Nunez. The book contains some simple statements which caught my attention:
- let’s go back to square 1
- let’s go forwards a couple steps
- there’s zero in the refrigerator
- this nullifies all that we have done
- Fred and Ginger danced as one
These metaphors imply that we understand numbers to operate as objects do or as movement does. These metaphors fascinated me and led me down a path to wanting to work with younger learners to understand how ideas of number are first experienced by learners. Several years on, I'm working with 6 year olds - a big change from 11-16 year olds back in the UK - and I've began working on trying to realise what these embodied metaphors mean for the learning of the mathematics which Lakoff and Nunez map these embodied metaphors to.
Last academic year, I worked with two movement (dance) teachers in my school and my class of 22 children. We spent an hour a week over 8 weeks with my class with the intention of supporting children to gain a deeper understanding of number using movement as a starting point.
Our basic lesson included a warm-up, proposals to the children to make a locomotor motion along with a drum pattern and then an invitation to draw the movements they had made on a roll of paper. We did this for about 6 weeks of the 8, allowing time for the class a couple lessons to learn the workings of the dance studio. Here are some drawings from 2 lessons.
Lesson 3 from 8:
Proposal: move to the drum (teacher counted and hit the drum from 1 to 8)
After the movement session we thought about the number pathways which we made with our bodies. The class were keen to make up some new pathways they could try out. And also tried to move to each other's drawn pathways.
One suggestion from a class member was to move more than one step at a time and so they drew pathways which showed jumps through space, using different numbers.
We had some discussion around numbers and what they were and different ways in which we experience them.
One student remarked:
When I was in group 2, I thought numbers were symbols that meant how many there were.
We had also previously established that numbers were symbols, words, names of numicon shapes and also meant how many once a set of objects was counted.
On another day, I asked the class: 'What is five?'
These responses included metaphors of movement.
It could be a pathway of 5. That it could go zig-zag then straight then curve then straight again.
Like this, this, this and then that (showing with her hands a movement).
5 is a pathway and a story.
Lesson 5 from 8:
Proposal: From a starting position, move 2 beats forwards. Move 6 beats backwards.
The first image in the selection of drawings was something we spoke about afterwards as a class. We then all tried to move the same pattern as the student who drew it. We talked about negative numbers and then made some more movements back in our classroom which explored forwards from the origin point (starting position) and then backwards through the origin.
From January, I intend to undertake the project again with my new class. Until then I have some reading and planning to carry out, to think about how the project extends into the classroom further. And to shape up more ideas of the role of movement in mathematics learning.
I really want to figure out which tasks can be set for students which can be carried out as group work. And which of these tasks lead to explorations and new realisations about the structure of the number system. I'm particularly excited by explorations of negative numbers and non-whole numbers; the latter was explored last year, but I don't have good documentation from those explorations which I can share.
Writing
I've had some excellent conversations recently with a colleague about how we achieve the holy grail of free writing from work with Cuisenaire Rods recently. We have looked at the work done by Gattegno and Goutard and Caroline Ainsworth and are trying to figure out how we make that work for our setting.
My colleague this week introduced notebooks for her class for their discoveries with rods. The invitation is for them to keep a note of their discoveries with the rods. Not missing a trick, I decided to do the same with my class.
We first spoke about discoveries from scientists and what they do with them. We talked about our discoveries with the rods and how we should remember them. Once motivated to keep a record of their discoveries, we got to trying to note them down in new special books for discoveries.
Children were encouraged to use whatever worked for them: pictures, words or symbols. We worked on writing without access to the concrete materials; this was a suggestion from Goutard. To work on the internalised and remembered structures and not to merely describe the concrete in front of them.
Here are 3 examples:
Six land
I'm a huge fan of Six-land, as proposed by Andrew Jeffrey. It is an imagined land in which things work in base-6. I worked with a group of children from a mix of classes (aged 6-8) and we have been figuring out how the number system works in six-land and also how to measure things.
One of the conversations we had was about how children who lived in six-land, learn how to use their numbers. A child suggested they had counting books... so we made some! Books that count in base-6. One of my favourites was one from a group who counted rocks and other natural things and made their book by photocopying them.

Equivalence game
Stolen from twitter: a game of equivalences using symmetry. Each student places a train of rods and then their partner aimed to place an equivalent train on their own side. I was surprised at how challenging this was for some students.